Image Registration
-
This section provides a step-by-step guide to register your new line or stain to the reference
zebrafish brain(as shown in Figure1) using Advanced
Normalization Tools
( ANTs). In order to get high quality mapping, you will
need to acquire high-quality
2-channel confocal stacks of your line. As use case we choose the Armin's Bahl 2P stack (as shown in Figure2)
and map it to reference brain. ANTs provide set of algorithms and metrics for registration
procedure. It is important that you should familiar with the basics of ANTs in order
to generate high quality mapping.
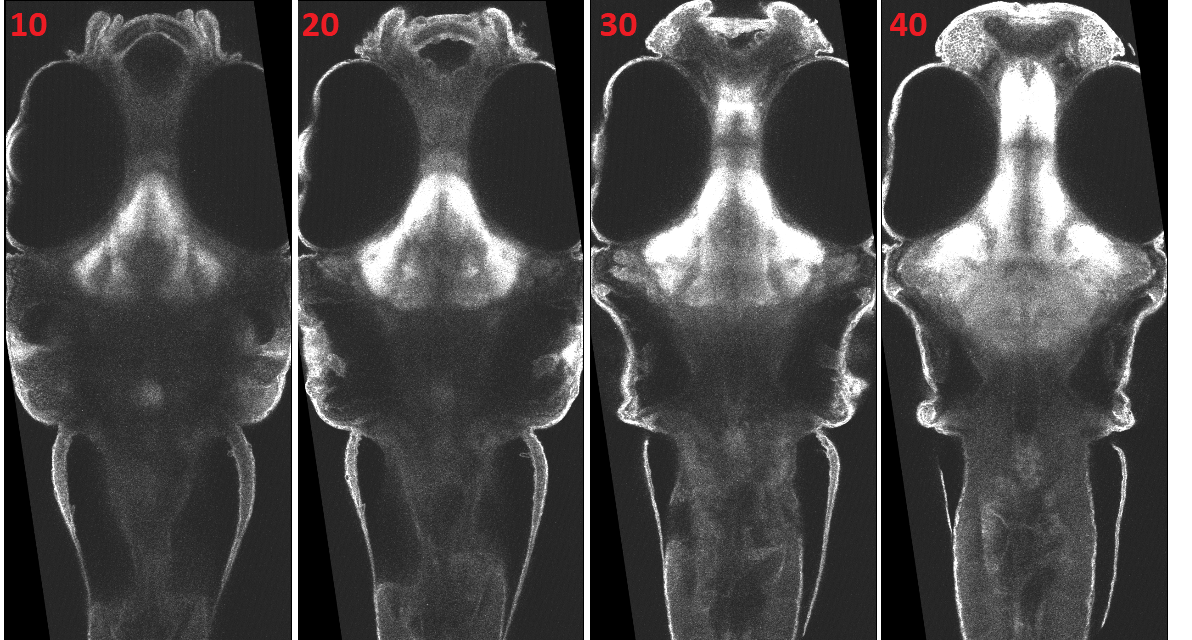
Figure1: Reference Zebrafish Brain 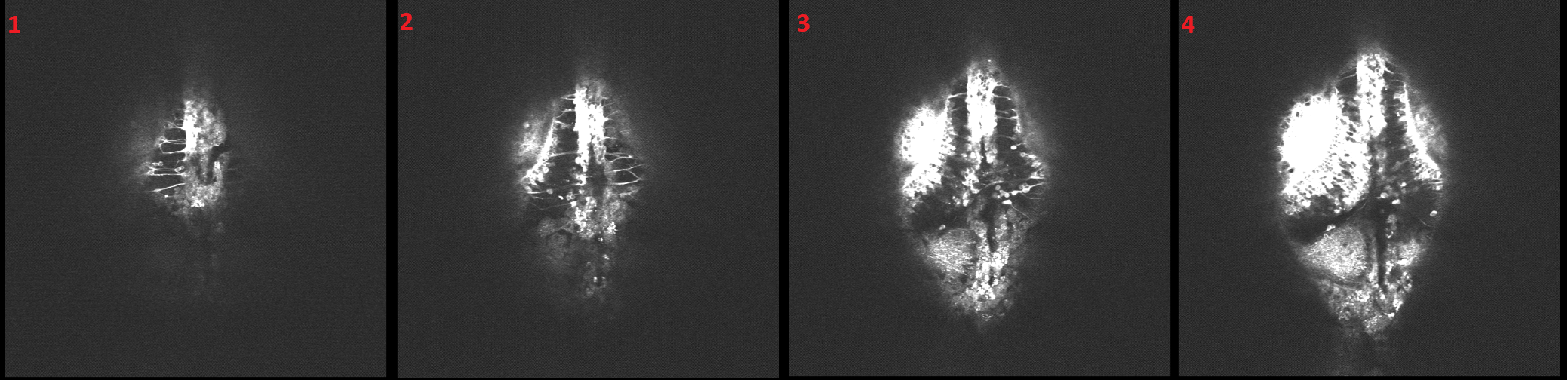
Figure2: 2P Stack
Following are the basics of ANTs to do the registration: -
The ANTs provide two set of algorithms : Linear and Non-linear Transforms.
Linear Registration: is mainly for rough alignment of dataset and offers following algorithms.- Translation.
- Rigid.
- Similarity.
- Affine.
- BSpline SyN.
- Geodesic SyN.
- Greedy SyN.
There is no standard algorithm that can solve all registration task. The choice of algorithm is totally dependent on dataset.
Similarity Metrics: It is the critical step in registration process which matches how well the target dataset is matched with referenced or fixed dataset. There is no fixed rule to select the metric, it totally depend on conditions like algorithm, dataset etc.
Generally, Mutal Information(MI) is preferred for linear transform and Cross-correlation(CC) is useful for fine scale non-linear registration step.- Mutal Information(MI)
- Cross-correlation(CC)
- Probabilistic Matching (PB)
- Mean Square Distance(MSQ)
- Point-set Expectation(PSE)
-
Following is the bash script for the image registration process:
#!/bin/bash # dim=3 # image dimensionality AP="" # /home/yourself/code/ANTS/bin/bin/ # path to ANTs binaries ITK_GLOBAL_DEFAULT_NUMBER_OF_THREADS=8 # controlling multi-threading export ITK_GLOBAL_DEFAULT_NUMBER_OF_THREADS f=$1 ; m=$2 # f: fixed or referenced image file m: moving image file or unregistered volume mysetting=$3 # current settings like testing or forproduction D=$4 #/home/image_registration/ # path to output directory if [[ ! -s $f ]] ; then echo no fixed $f ; exit; fi if [[ ! -s $m ]] ; then echo no moving $m ;exit; fi if [[ ${#mysetting} -eq 0 ]] ; then echo usage is echo $0 fixed.nii.gz moving.nii.gz mysetting echo where mysetting is either forproduction or testing exit fi nm1=` basename $f | cut -d '.' -f 1 ` nm2=` basename $m | cut -d '.' -f 1 ` reg=${AP}antsRegistration # path to antsRegistration if [[ $mysetting == "testing" ]] ; then its=200x200x200 percentage=0.2 syn="20x20x0,1.e-8,5" else its=100x100x100 percentage=0.25 syn="100x100x50,1.e-8,5" mysetting=forproduction fi echo affine $m $f outname is $nm am using setting $mysetting nm=${D}${nm1}_fixed_${nm2}_moving_setting_is_${mysetting} # construct output prefix $reg -d $dim -r [ $f, $m ,1] \ -m mattes[ $f, $m , 1 , 32, regular, $percentage ] \ -t translation[ 0.1 ] \ -c [$its,1.e-8,20] \ -s 4x2x1vox \ -f 6x4x2 -l 1 \ -m mattes[ $f, $m , 1 , 32, regular, $percentage ] \ -t rigid[ 0.1 ] \ -c [$its,1.e-8,20] \ -s 4x2x1vox \ -f 3x2x1 -l 1 \ -m mattes[ $f, $m , 1 , 32, regular, $percentage ] \ -t affine[ 0.1 ] \ -c [$its,1.e-8,20] \ -s 4x2x1vox \ -f 3x2x1 -l 1 \ -m mattes[ $f, $m , 0.5 , 32 ] \ -m cc[ $f, $m , 0.5 , 4 ] \ -t SyN[ .1, 3, 0 ] \ -c [ $syn ] \ -s 4x2x1vox \ -f 4x2x1 -l 1 -u 1 -z 1 \ -o [${nm},${nm}_diff.nii.gz,${nm}_inv.nii.gz] ${AP}antsApplyTransforms -d $dim -i $m -r $f -n linear -t ${nm}1Warp.nii.gz -t ${nm}0GenericAffine.mat -o ${nm}_warped.nii.gz
-
Following are the list of parameters that are used in the above registration script and their
detailed description:
Finally, following are the slices of the registered image stack.Parameter Name Description f Fixed or reference brain m Moving file or unregistered volume t Tranformation algorithms like rigid, translation etc Iterations(its) Iterations per scale for affine step percentage percentage of voxels sampled for evaluating the metric SyN(syn) used only for non-linear tranfomation and consist of iteration steps per sample and stopping criteria like 1e-8 or 1e-7 Smoothing Factor(f) is used for smoothing the down-sampled image with gaussian kernel. This parameter is dependent on the shrinking factor. For example if the shrinking factor is 2 then smoothing factor will be 0.2
Formula used: (shrinking factor[d] -1)*0.2.Shrinking Factor(s) is used for down-sampling an unregistered image. They are forming a kind of image pyramid for unregistered image and apply the above algorithms on each of the image in the pyramid. Shrinking factor is totally depend on the size of your image stack. For example: 700x700x29 is the size of our 2P stack and 4x2x1 is the shrinking factor. It will down-sample the image by factor of 4x4x4 , 2x2x2 and 1x1x1. One should be careful in setting this parameter because it also checks length of minimum dimension i.e 29 in our case because if you downscale such a small z by power of 8 or more. we will left with almost nothing and lot of resources will be wasted. It should also be power of 2 like 2,4,8,16,32 etc.In most of the scenarios, down-sampling upto 8 is enough. 
Figure3: Registered 2P Stack
-
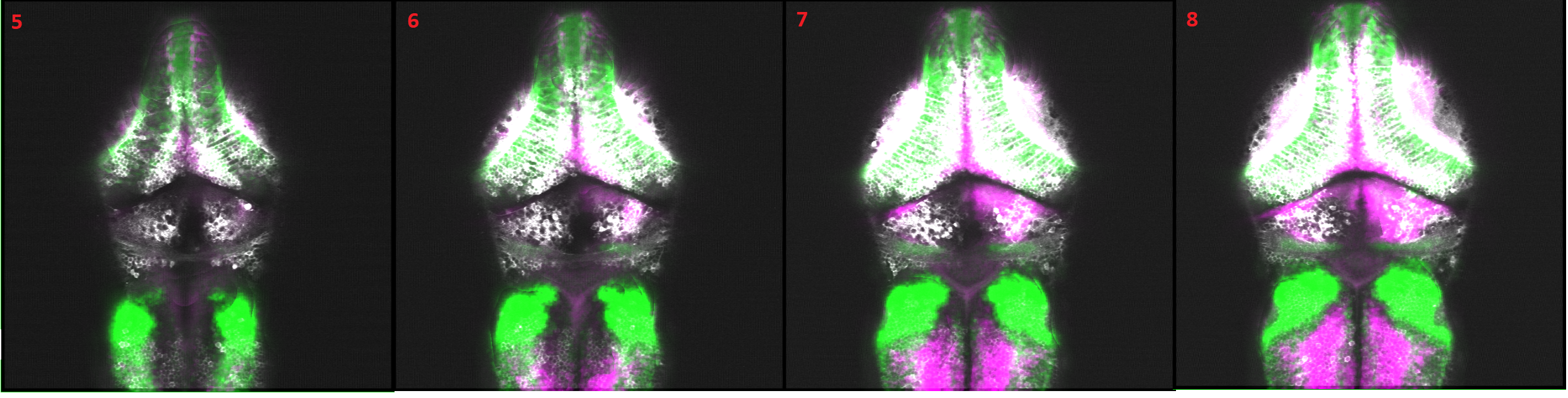
Imagine now that you want to do the inverse mapping i.e. you will take any mapped stack from the reference brain, or an empty stack with the Owen - masks, and transform that into your stack e.g. 2P stack and overlay. This allows you to immediately visualize neuro transmitter identity and brain regions together with planer neural activity. Here is an example stack, where we used the inverted mapping to map the zbrain vglut stack as well as the zbrain gadb1 stack into 2P stack. This registration reveals the pattern of excitatory and inhibitory cells within each imaged plane as shown below.
Finally, following are the slices of the registered image stack.